主题
背包问题
背包九讲 -- 01背包问题
特点
- 每个数只能用一次
- 物品一个一个选,容量也一点一点增加去考虑
状态:
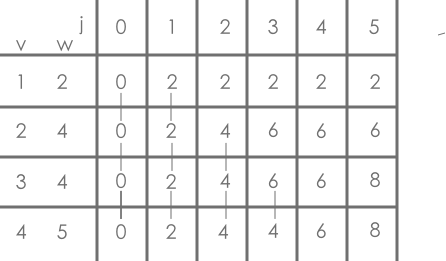
dp[i][j]表示在只能选择前i个物品,背包容量为j的情况下,背包中物品的最大价值方程
背包容量放不下物品(j < v[i]),则被迫不能选,即下图有竖线的,表示直接继承上面的
dp[i][j] = dp[i - 1][j]背包容量放的下物品,则取 不选择和选择 两个选择中的最大价值的
dp[i][j] = max{dp[i - 1][j], dp[i - 1][j - v[i]]}
$$ dp[i][j] = \begin{cases} dp[i - 1][j], & \text {j $\lt$ v[i]} \ max{dp[i - 1][j], , dp[i - 1][j - v[i]] }, & \text{j $\geq$ v[i]} \end{cases} $$
java
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt(); // 物品总数量
int v = scanner.nextInt(); // 背包可承受的总重量
int[] vs = new int[n], ws = new int[n]; // vs:物品的重量 ws:物品的价值
for (int i = 0; i < n; i++) {
vs[i] = scanner.nextInt();
ws[i] = scanner.nextInt();
}
scanner.close();
int[][] dp = new int[n + 1][v + 1];
for (int i = 1; i <= n; i++) { // 物品
for (int j = 0; j <= v; j++) { // 重量
if (j >= vs[i - 1]) {
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - vs[i - 1]] + ws[i - 1]);
} else {
dp[i][j] = dp[i - 1][j];
}
}
}
System.out.println(dp[n][v]);
}
}可观察到,和最小路径一样,也是逐个填写,故空间可降维,但后面列依赖前面列,所以要列需要倒序填表
java
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int v = scanner.nextInt();
int[] vs = new int[n], ws = new int[n];
for (int i = 0; i < n; i++) {
vs[i] = scanner.nextInt();
ws[i] = scanner.nextInt();
}
scanner.close();
int[] dp = new int[v + 1];
for (int i = 0; i < n; i++) { // 物品
for (int j = v; j >= vs[i]; j--) { // 重量,倒序,这样就可以拿到上一行前面列的结果
dp[j] = Math.max(dp[j], dp[j - vs[i]] + ws[i]);
}
}
System.out.println(dp[v]);
}
}01背包--分割等和子集(416)
- 状态:
dp[i]在只能选择前i个物品,背包容量为j的情况下,背包中物品的和是否恰好等于背包容量的一半 - 方程
$$ dp[i][j] = \begin{cases} dp[i - 1][j], & \text {j $\lt$ nums[i]} \ dp[i - 1][j] , || , dp[i - 1][j - v[i]], & \text{j $\geq$ nums[i]} \end{cases} $$
java
public boolean canPartition(int[] nums) {
int total = 0;
for (int num : nums) total += num;
if (total % 2 == 1) return false; // 如果为总和为奇数,则返回 false
int v = total / 2, n = nums.length; // v:背包总重量 n:物品数量
boolean[][] dp = new boolean[n + 1][v + 1];
dp[0][0] = true; // 不符合状态定义,但有利于后面状态的计算
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= v; j++) {
if (j < nums[i - 1]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i - 1]];
}
if (dp[i][v]) return true; // 由于状态转移方程的特殊性,提前结束,可以认为是剪枝操作
}
return dp[n][v];
}降维
java
public boolean canPartition(int[] nums) {
int total = 0;
for (int num : nums) total += num;
if (total % 2 == 1) return false; // 如果为总和为奇数,则返回 false
int v = total / 2, n = nums.length; // v:背包总重量 n:物品数量
boolean[] dp = new boolean[v + 1];
dp[0] = true; // 不符合状态定义,但有利于后面状态的计算
for (int i = 0; i < n; i++) { // 物品
for (int j = v; j >= nums[i]; j--) { // 重量
dp[j] = dp[j] || dp[j - nums[i]];
}
if (dp[v]) return true; // 由于状态转移方程的特殊性,提前结束,可以认为是剪枝操作
}
return dp[v];
}01背包--一和零(474)
- 状态:
dp[i][j][k]表示输入字符串在子区间[0, i]能够使用j个0和k个1的字符串的最大数量 - 方程
$$ dp[i][j][k] = \begin{cases} dp[i - 1][j][k], & \text {j $\lt$ 0的个数 && k $\lt$ 1的个数} \ max{dp[i - 1][j][k], ,, dp[i - 1][j - 0的个数][k - 1的个数] + 1 }, & \text{j $\geq$ 0的个数 && k $\geq$ 1的个数} \end{cases} $$
java
public int findMaxForm(String[] strs, int m, int n) {
int len = strs.length;
int[][][] dp = new int[len + 1][m + 1][n + 1];
for (int i = 1; i <= len; i++) {
int[] arr = getZeroAndOne(strs[i - 1]); // 获取当前字符串 0 1 个数
for (int j = 0; j <= m; j++) {
for (int k = 0; k <= n; k++) {
if (j >= arr[0] && k >= arr[1]) {
dp[i][j][k] = Math.max(dp[i - 1][j][k], dp[i - 1][j - arr[0]][k - arr[1]] + 1);
} else {
dp[i][j][k] = dp[i - 1][j][k];
}
}
}
}
return dp[len][m][n];
}
private int[] getZeroAndOne(String s) {
int[] res = new int[2];
for (char c : s.toCharArray()) {
res[c - '0']++;
}
return res;
}降维
java
public int findMaxForm(String[] strs, int m, int n) {
int[][] dp = new int[m + 1][n + 1];
for (String s : strs) {
int[] arr = getZeroAndOne(s);
for (int i = m; i >= arr[0]; i--) {
for (int j = n; j >= arr[1]; j--) {
dp[i][j] = Math.max(dp[i][j], dp[i - arr[0]][j - arr[1]] + 1);
}
}
}
return dp[m][n];
}
private int[] getZeroAndOne(String s) {
int[] res = new int[2];
for (char c : s.toCharArray()) {
res[c - '0']++;
}
return res;
}01背包--目标和(494)
状态:
dp[i][j]表示在数组 nums 的前 i 个数中选取元素,使得这些元素之和等于 j 的方案数方程
记数组的元素和为 sum,添加 - 号的元素和为 x,则其余添加 + 的元素和为 sum - x,则有
$$ (sum - x) - x = target \ sum - 2x = target \ x = sum - target / 2 $$
上述成立的前提是 sum - target 是非负偶数,不符合条件可直接返回 0
java
public int findTargetSumWays(int[] nums, int target) {
int total = 0;
for (int num : nums) total += num;
int diff = total - target;
if (diff < 0 || diff % 2 == 1) return 0;
int n = nums.length, v = diff / 2;
int[][] dp = new int[n + 1][v + 1];
dp[0][0] = 1; // 当个数为0,背包容量为0时,也是一种
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= v; j++) {
if (j >= nums[i - 1]) {
dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i - 1]];
} else {
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[n][v];
}降维
java
public int findTargetSumWays(int[] nums, int target) {
int total = 0;
for (int num : nums) total += num;
int diff = total - target;
if (diff < 0 || diff % 2 == 1) return 0;
int v = diff / 2;
int[] dp = new int[v + 1];
dp[0] = 1;
for (int num : nums) {
for (int i = v; i >= num; i--) {
dp[i] = dp[i] + dp[i - num];
}
}
return dp[v];
}背包九讲--完全背包问题
特点
- 物品可以使用多次
- 不计算顺序,如 [1, 5, 1] 和 [5, 1, 1] 是同一种结果
- 状态:
dp[i][j]表示在只能选择前i个物品(物品可以多次选择),背包容量为j的情况下,背包中物品的最大价值 - 方程
- 先继承上一件物品的选择,
dp[i][j] = dp[i - 1][j] - 然后看放 1...n 件物品的总价值,哪个最大
- 先继承上一件物品的选择,
java
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int v = scanner.nextInt();
int[] vs = new int[n], ws = new int[n];
for (int i = 0; i < n; i++) {
vs[i] = scanner.nextInt();
ws[i] = scanner.nextInt();
}
scanner.close();
int[][] dp = new int[n + 1][v + 1];
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= v; j++) {
dp[i][j] = dp[i - 1][j];
// 找 dp[i][j] 这个格子,放 k 件同一个物品的最大值
for (int k = 1; j - k * vs[i - 1] >= 0; k++) {
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - k * vs[i - 1]] + k * ws[i - 1]);
}
}
}
System.out.println(dp[n][v]);
}
}因为二层循环,前面的 j,其实已经记录了放相同物品, 1...k-1 件时的最大值了,所以放 k 件相同物品时,可以基于 j - k * 重量 来计算,省去一层循环
java
int[][] dp = new int[n + 1][v + 1];
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= v; j++) {
dp[i][j] = dp[i - 1][j];
if (j >= vs[i - 1]) {
dp[i][j] = Math.max(dp[i][j], dp[i][j - vs[i - 1]] + ws[i - 1]);
}
}
}和 01背包 相似,i 是基于 i-1 更新的,所以完全可以降维,不过 j 是基于前面的 j 更新的,所以是二层循环是正序
java
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int v = scanner.nextInt();
int[] vs = new int[n], ws = new int[n];
for (int i = 0; i < n; i++) {
vs[i] = scanner.nextInt();
ws[i] = scanner.nextInt();
}
scanner.close();
int[] dp = new int[v + 1];
for (int i = 0; i < n; i++) {
for (int j = vs[i]; j <= v; j++) { // 正序,因为后面格子需要依赖前面的格子
dp[j] = Math.max(dp[j], dp[j - vs[i]] + ws[i]);
}
}
System.out.println(dp[v]);
}
}完全背包--零钱充换(322)
- 状态:
dp[i][j]表示在数组 icons 的前 i 个数中选取元素,使得这些元素之和等于 j 的最少硬币数
java
public int coinChange(int[] coins, int amount) {
int n = coins.length;
int[][] dp = new int[n + 1][amount + 1];
for (int[] d : dp) Arrays.fill(d, amount + 1);
dp[0][0] = 0;
for (int i = 1; i <= n; i++) { // 物品
for (int j = 0; j <= amount; j++) { // 背包容量
dp[i][j] = dp[i - 1][j];
for (int k = 1; j - k * coins[i - 1] >= 0; k++) { // 放 k 枚硬币进背包里
dp[i][j] = Math.min(dp[i][j], dp[i][j - k * coins[i - 1]] + k);
}
}
}
return dp[n][amount] == amount + 1 ? -1 : dp[n][amount];
}去除第三层循环
java
for (int i = 1; i <= n; i++) { // 物品
for (int j = 0; j <= amount; j++) { // 背包容量
dp[i][j] = dp[i - 1][j];
if (j >= coins[i - 1]) { // 基于前面的 j 更新后面的 j
dp[i][j] = Math.min(dp[i][j], dp[i][j - coins[i - 1]] + 1);
}
}
}降维
java
public int coinChange(int[] coins, int amount) {
int n = coins.length;
int[] dp = new int[amount + 1];
Arrays.fill(dp, amount + 1);
dp[0] = 0;
for (int coin : coins) {
for (int i = coin; i <= amount; i++) {
dp[i] = Math.min(dp[i], dp[i - coin] + 1);
}
}
return dp[amount] == amount + 1 ? -1 : dp[amount];
}完全背包--零钱充换2(518)
- 状态:
dp[i][j]表示在数组 icons 的前 i 个数中选取元素,使得这些元素之和等于 j 的方案数
java
public int change(int amount, int[] coins) {
int n = coins.length;
int[][] dp = new int[n + 1][amount + 1];
dp[0][0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= amount; j++) {
dp[i][j] = dp[i - 1][j];
for (int k = 1; j - k * coins[i - 1] >= 0; k++) {
dp[i][j] += dp[i - 1][j - k * coins[i - 1]];
}
}
}
return dp[n][amount];
}去除第三层循环
java
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= amount; j++) {
dp[i][j] = dp[i - 1][j];
if (j >= coins[i - 1]) {
dp[i][j] += dp[i][j - coins[i - 1]];
}
}
}降维
java
public int change(int amount, int[] coins) {
int n = coins.length;
int[] dp = new int[amount + 1];
dp[0] = 1;
for (int coin : coins) {
for (int i = coin; i <= amount; i++) {
dp[i] += dp[i - coin];
}
}
return dp[amount];
}