主题
岛屿类题目
DFS 解法的三要素
访问相邻节点,放在图的 DFS 上,就是上、下、左、右四个方向的节点
js
// 定义上下左右四个方向的方向变量
const dx = [0, 0, 1, -1]
const dy = [1, -1, 0, 0]
function dfs(y, x) {
// ...
for (let i = 0; i < 4; i++) {
dfs(y + dy[i], x + dx[i])
}
}避免图的重复遍历
以下这种情况,DFS 就会一直兜圈子,陷入死循环
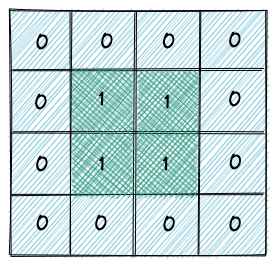
所以需要记录已经走过的节点,每走过一个陆地格子,就把格子的值改为 2,这样再遇到 2 的时候,就知道这是遍历过的格子了
js
function dfs(y, x) {
if (g[y][x] === 2) return
g[y][x] = 2
}base case
- 发现超出了网格范围
- 发现超出了陆地范围(不同题目,这个 base case 可能不成立)
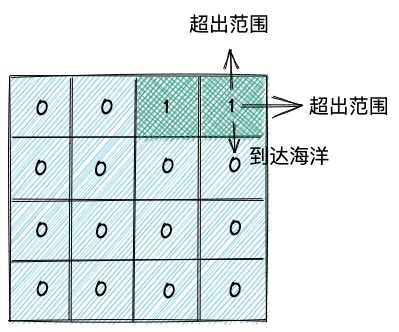
js
function dfs(y, x) {
if (y < 0 || x < 0 || y >= r || x >= c || g[y][x] === 0) return
}综上所述,得到一个岛屿问题的额 DFS 遍历框架
js// 定义上下左右四个方向的方向变量 const dx = [0, 0, 1, -1] const dy = [1, -1, 0, 0] function dfs(y, x) { // 1. 超出范围 // 2. 已经走过了或者到达海洋 if (y < 0 || x < 0 || y >= r || x >= c || g[y][x] !== 1) return g[y][x] = 2 for (let i = 0; i < 4; i++) { dfs(y + dy[i], x + dx[i]) } }
200. 岛屿数量
js
const dx = [0, 0, 1, -1]
const dy = [1, -1, 0, 0]
let r, c, g
var numIslands = function(grid) {
g = grid
r = grid.length
c = grid[0].length
let count = 0 // 岛屿数量
for (let y = 0; y < r; y++) {
for (let x = 0; x < c; x++) {
if (g[y][x] === "1") {
dfs(y, x)
count++ // 每一次 dfs 都是一个岛屿
}
}
}
return count
};
function dfs(y, x) {
if (x < 0 || x >= c || y < 0 || y >= r || g[y][x] !== '1') {
return
}
g[y][x] = '2'
for (let i = 0; i < 4; i++) {
dfs(y + dy[i], x + dx[i])
}
}463. 岛屿的周长
往四个方向遍历时,遇到边界与海洋,都能让周长+1,但如果是岛屿则不算周长
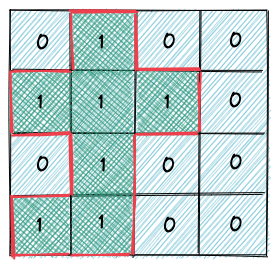
js
const dx = [0, 0, 1, -1]
const dy = [1, -1, 0, 0]
let r, c, g
var islandPerimeter = function(grid) {
g = grid
r = g.length
c = g[0].length
for (let y = 0; y < r; y++) {
for (let x = 0; x < c; x++) {
if (g[y][x] === 1) {
return dfs(y, x)
}
}
}
return 0
};
function dfs(y, x) {
// 边界与海洋
if (y < 0 || x < 0 || y >= r || x >= c || g[y][x] === 0) {
return 1
}
// 遍历过的陆地
if (g[y][x] === 2) return 0
g[y][x] = 2
let count = 0
for(let i = 0; i < 4; i++) {
count += dfs(y + dy[i], x + dx[i])
}
return count
}695. 岛屿的最大面积
js
const dx = [0, 0, 1, -1]
const dy = [1, -1, 0, 0]
let r, c, g
var maxAreaOfIsland = function(grid) {
g = grid
r = g.length
c = g[0].length
let max = 0
for (let y = 0; y < r; y++) {
for (let x = 0; x < c; x++) {
if (g[y][x] === 1) {
max = Math.max(max, dfs(x, y))
}
}
}
return max
};
function dfs(x, y) {
if (x < 0 || y < 0 || x >= c || y >= r || g[y][x] !== 1) {
return 0
}
g[y][x] = 2
let count = 1 // 岛屿本身算一个面积
for (let i = 0; i < 4; i++) {
count += dfs(x + dx[i], y + dy[i])
}
return count
}827. 最大人工岛
岛屿最大面积问题的升级版,可以把一个海洋格子变成陆地格子,进而让两块岛屿连成一块
先计算出所有岛屿的面积,在所有的格子上标记出岛屿的面积。然后搜索哪个海洋格子相邻的两个岛屿面积最大
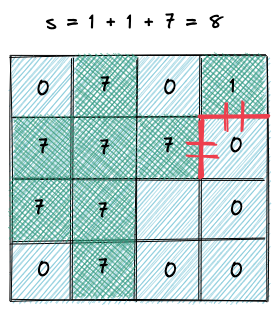
但这样做会有一个问题,如下图的海洋格子,这时候连接成的岛屿面积是 7 + 1 + 7 吗?,显然不是,这两个 7 来自同一个岛屿,所以填海造陆之后得到的岛屿面积应该只有 7 + 1 = 8
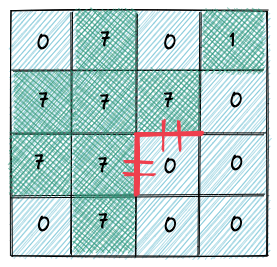
所以不能直接在标记陆地格子的面积,而是应该建立一个哈希表,记录一个唯一 key 与面积的对应关系,然后在陆地格子上标记 key
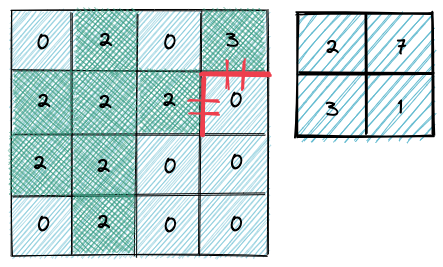
这道题要做两次搜索,第一次 DFS 遍历陆地格子,计算每个岛屿的面积并标记岛屿。第二次遍历海洋格子,观察每个海洋格子相邻的陆地格子
js
const dx = [0, 0, 1, -1]
const dy = [1, -1, 0, 0]
let r, c, g, s
var largestIsland = function(grid) {
g = grid
r = g.length
c = g[0].length
s = {} // 哈希表
let max = 0 // 最大的岛屿面积,防止没有海洋节点的情况
let n = 2 // 哈希表的 key
// 计算每个岛屿的面积并标记岛屿
for (let y = 0; y < r; y++) {
for (let x = 0; x < c; x++) {
if (g[y][x] === 1) {
s[n] = dfs(x, y, n)
max = Math.max(max,s[n])
n++
}
}
}
// 填海造陆
for (let y = 0; y < r; y++) {
for (let x = 0; x < c; x++) {
if (g[y][x] === 0) {
max = Math.max(max, fill(x, y))
}
}
}
return max
};
function dfs(x, y, n) {
if (x < 0 || y < 0 || x >= c || y >= r || g[y][x] !== 1) {
return 0
}
g[y][x] = n
let count = 1
for (let i = 0; i < 4; i++) {
count += dfs(x + dx[i], y + dy[i], n)
}
return count
}
function fill(x, y) {
const used = [] // 记录已经找过岛屿的 key
let count = 1 // 填海后本身有一个面积
for(let i = 0; i < 4; i++) {
const nx = x + dx[i], ny = y + dy[i]
if (nx < 0 || ny < 0 || nx >= c || ny >= r || g[ny][nx] === 0) {
continue
}
// 已经找过这个岛屿了,则跳过
if (used.includes(g[ny][nx])) continue
used.push(g[ny][nx])
count += s[g[ny][nx]]
}
return count
}