排列组合子集类题目

递归树与解法

组合/子集

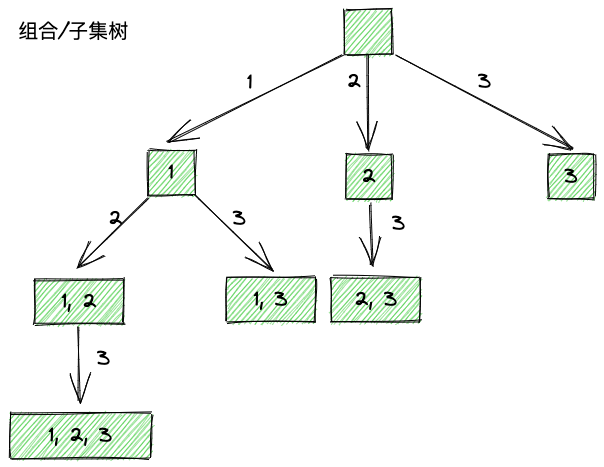
1. 无顺序，[1, 2] 和 [2, 1] 是同一种子集

2. 使用 start 记录当前选择列表的起始位置，比如 [2] 这条路径，后面只有 3 选择，所以下一次递归，选择应该从 3 开始

排列

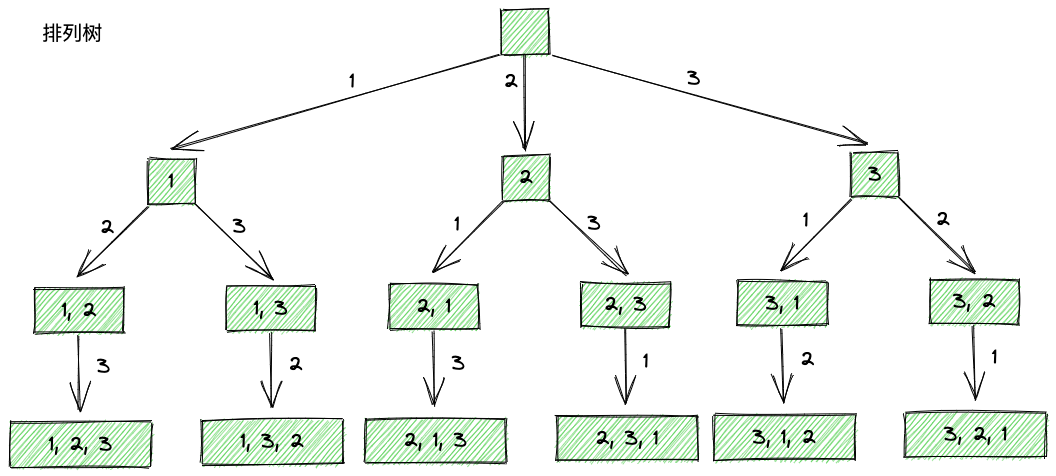
1. 有顺序，[1, 2] 和 [2, 1] 不是同一种排列
2. 使用 used 布尔数组记录已经选择过的元素，下次递归时，如果选择过了，则跳过

元素无重不可复选

子集：78. 子集

function subsets(nums: number[]): number[][] {
    const res = [], len = nums.length
    const dfs = (start: number, path: number[]) => {
        res.push([...path]) // 复制一份 path，放入结果集中
        for (let i = start; i < len; i++) {
            // 做选择
            path.push(nums[i])
            // 通过 start 参数控制树枝的遍历，避免产生重复的子集
            dfs(i + 1, path)
            // 撤销选择
            path.pop()
        }
    }
    dfs(0, [])
    return res
}

组合：77. 组合

返回 k 个数的组合，其实就是在全子集内选择第 k 层的子集

function combine(n: number, k: number): number[][] {
    const res = []
    const dfs = (start: number, path: number[]) => {
        // 只要第 k 层的
        if (path.length === k) {
            res.push([...path]) // 复制一份 path，放入结果集中
        }

        for (let i = start; i <= n; i++) {
            // 做选择
            path.push(i)
            // 通过 start 参数控制树枝的遍历，避免产生重复的子集
            dfs(i + 1, path)
            // 撤销选择
            path.pop()
        }
    }
    dfs(1, [])
    return res
}

排列：46. 全排列

function permute(nums: number[]): number[][] {
    const res: number[][] = [], len = nums.length, used: boolean[] = Array(len).fill(false)

    const dfs = (path: number[]) => {
        if (path.length === len) {
            res.push([...path])
            return
        }

        for (let i = 0; i < len; i++) {
            if (used[i]) continue
            // 做选择
            used[i] = true
            path.push(nums[i])
            // 进入下一层回溯树
            dfs(path)
            // 取消选择
            used[i] = false
            path.pop()
        }
    }

    dfs([])
    return res
}

元素可重不可复选

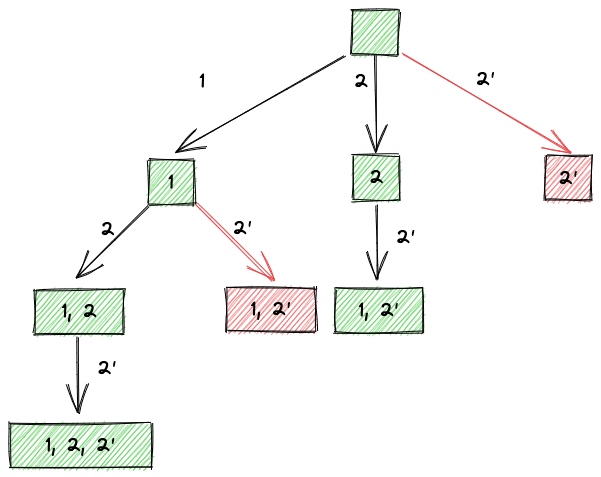
子集：90. 子集II

某一次递归，选择时，相同的值，只取第一次的

function subsetsWithDup(nums: number[]): number[][] {
    const res: number[][] = []
    nums.sort((a, b) => a - b) // 先排序，让相同的元素靠在一起

    const dfs = (index: number, path: number[]) => {
        res.push([...path])

        for (let i = index; i < nums.length; i++) {
            // 剪枝逻辑，值相同的相邻树枝，只遍历第一条
            if (i > index && nums[i] === nums[i - 1]) continue
            path.push(nums[i])
            dfs(i + 1, path)
            path.pop()
        }
    }

    dfs(0, [])
    return res
}

组合：40. 组合总和 II

function combinationSum2(candidates: number[], target: number): number[][] {
    const res: number[][] = []
    candidates.sort((a, b) => a - b) // 先排序，让相同的元素靠在一起

    const dfs = (index: number, path: number[], sum: number) => {
        // 达到目标和，找到符合条件的组合
        if (sum === target) {
            res.push([...path])
            return
        }
         // 超过目标和，直接结束
        if (sum > target) return

        for (let i = index; i < candidates.length; i++) {
            // 剪枝逻辑，值相同的树枝，只遍历第一条
            if (i > index && candidates[i] === candidates[i - 1]) continue
            path.push(candidates[i])
            dfs(i + 1, path, sum + candidates[i])
            path.pop()
        }
    }

    dfs(0, [], 0)
    return res
}

排列：47. 全排列 II

function permuteUnique(nums: number[]): number[][] {
    const res: number[][] = [], len = nums.length, used: boolean[] = Array(len).fill(false)
    nums.sort((a, b) => a - b) // 先排序，让相同的元素靠在一起

    const dfs = (path: number[]) => {
        if (path.length === len) {
            res.push([...path])
            return
        }

        for (let i = 0; i < len; i++) {
            if (used[i]) continue
            // 新添加的剪枝逻辑，固定相同的元素在排列中的相对位置
            if (i !== 0 && nums[i] === nums[i - 1] && !used[i - 1]) continue

            used[i] = true
            path.push(nums[i])
            dfs(path)
            path.pop()
            used[i] = false
        }
    }

    dfs([])
    return res
}

理解 !usedp[i - 1] 的判断逻辑

假设输入为 nums = [2, 2']，标准的全排列为 [2, 2']，[2', 2]

但在 全排列2 里，这个结果是重复的，[2, 2']，[2', 2] 被算为同一个排列

标准全排列算法之所以出现重复，是因为把相同元素形成的排列序列视为不同的序列，但实际上它们应该是相同的

如何设计剪枝逻辑，把这种重复去除掉？

答案是，保证相同元素在排列中的相对位置保持不变。

比如上面的 [2', 2] 的相对位置就变了，这种就应该被剪枝

反应到代码就是 2 还没被选择，2' 就要被选择了，所以当 nums[i] === nums[i - 1] && !used[i - 1] 就要被剪枝

无重可复选

子集：39. 组合总和

这道题说是组合问题，实际上也是子集问题：candidates 的哪些子集的和为 target？

// 子集问题是如何保证无重的：下一次递归从 i + 1 起
dfs(i + 1)

那么想要可重复选择同一个元素，下一层只要从让 start = i 即可

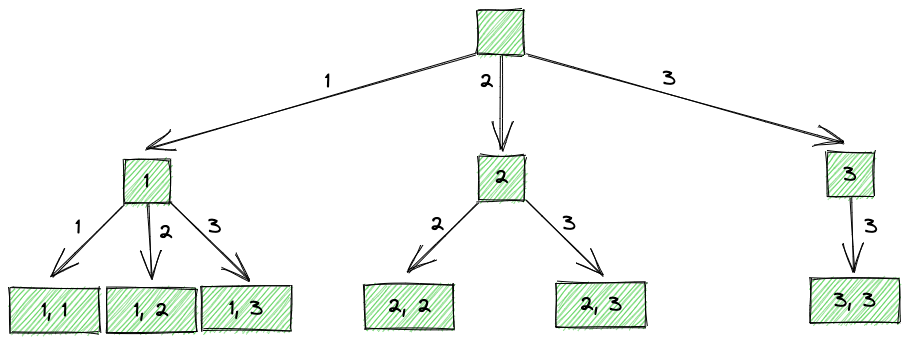
但这样会无限递归，所以路径和大于 target 时就没必要再遍历下去了

function combinationSum(candidates: number[], target: number): number[][] {
    const res: number[][] = []

    const dfs = (index: number, path: number[], sum: number) => {
        if (sum === target) {
            res.push([...path])
            return
        }

        if (sum > target) return

        for (let i = index; i < candidates.length; i++) {
            path.push(candidates[i])
            // 同一元素可重复使用，注意参数
            dfs(i, path, sum + candidates[i])
            path.pop()
        }
    }

    dfs(0, [], 0)
    return res
}

排列

leetcode 没有类似的题目

其实也是去除限制选择重复元素的逻辑即可，即去除 used

function dfs(path, nums, res) {
  const len = nums.length
  if (path.length === len) {
    res.push([...path])
  }

  for (let i = 0; i < len; i++) {
    path.push(nums[i])
    // 进入下一层回溯树
    dfs(path, nums, res)
    path.pop()
  }
}